IF YOU FIND THE AREA........LETS WATCH....

MORE ABOUT AREA AND PERIMETER

http://www.bgfl.org/custom/resources_ftp/client_ftp/ks2/maths/perimeter_and_area/index.html

AREA

Area of a Square The area of a square that has a side-length of 1 cm is 1 square centimetre (or 1 cm2).  To find the area of a square by the method of counting squares, we divide the square into smaller squares of one centimetre side-length . Consider a square that has a side-length of 4 cm. 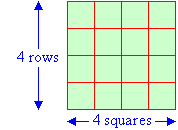Using the method of counting squares, we find that the area of the square is 16 cm2. Clearly, the square contains 4 rows of 4 squares.  Therefore: This suggests that: The area of a square is equal to its side-length multiplied by its side-length.  That is: Using the pronumerals A for area and s for side-length, we can write it simply as: This is the formula for the area of a square. Example 1 Find the area of a square flower-bed of side 15 m. Solution:
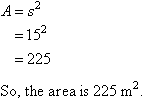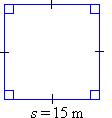Note: To find the area of a region enclosed within a plane figure, draw a diagram and write an appropriate formula.  Then substitute the given values and use a calculator, if necessary, to obtain the required area.

Perimeter

A square and an equilateral triangle are both examples of regular polygons. Another method for finding the perimeter of a regular polygon is to multiply the number of sides by the length of one side. Let's revisit Examples 3 and 4 using this second method.
Example 3:	Find the perimeter of a square with each side measuring 2 inches.
Solution:	This regular polygon has 4 sides, each with a length of 2 inches. Thus we get:
	= 4(2 in) = 8 in
Example 4:	Find the perimeter of an equilateral triangle with each side measuring 4 centimeters.
Solution:	This regular polygon has 3 sides, each with a length of 4 centimeters. Thus we get:
	= 3(4 cm) = 12 cm
Example 5:	Find the perimeter of a regular pentagon with each side measuring 3 inches.
Solution:	= 5(3 in) = 15 in
Example 6:	The perimeter of a regular hexagon is 18 centimeters. How long is one side?
Solution:	= 18 cm
	Let  represent the length of one side. A regular hexagon has 6 sides, so we can divide the perimeter by 6 to get the length of one side ().
	= 18 cm ÷ 6
	= 3 cm
Summary:	To find the perimeter of a polygon, take the sum of the length of each side. The formula for perimeter of a rectangle is: . To find the perimeter of a regular polygon, multiply the number of sides by the length of one side.

Perimeter Part I

The perimeter of a polygon is the distance around the outside of the polygon. A polygon is 2-dimensional; however, perimeter is 1-dimensional and is measured in linear units. To help us make this distinction, look at our picture of a rectangular backyard. The yard is 2-dimensional: it has a length and a width. The amount of fence needed to enclose the backyard (perimeter) is 1-dimensional. The perimeter of this yard is the distance around the outside of the yard, indicated by the red arrow; It is measured in linear units such as feet or meters.
To find the perimeter of a polygon, take the sum of the length of each side. The polygons below are much smaller than a fenced-in yard. Thus, we use smaller units in our examples, such as centimeters and inches.
Example 1:	Find the perimeter of a triangle with sides measuring 5 centimeters, 9 centimeters and 11 centimeters.
Solution:	P = 5 cm + 9 cm + 11 cm = 25 cm
Example 2:	A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the perimeter.
Solution 1:	P = 8 cm + 8cm + 3 cm + 3 cm = 22 cm
Solution 2:	P = 2(8 cm) + 2(3 cm) = 16 cm + 6 cm = 22 cm
In Example 2, the second solution is more commonly used. In fact, in mathematics, we commonly use the following formula for perimeter of a rectangle: ,  where  is the perimeter,  is the length and  is the width.
In the next few examples, we will find the perimeter of other polygons.
Example 3:	Find the perimeter of a square with each side measuring 2 inches.
Solution:	= 2 in + 2 in + 2 in + 2 in = 8 in
Example 4:	Find the perimeter of an equilateral triangle with each side measuring 4 centimeters.
Solution:	= 4 cm + 4 cm + 4 cm = 12 cm

Perimeter worksheet 1

Remember: Perimeter is the total distance around the outside of a 2D shape.You calculate it by adding together all the lengths of a shape.

Work out the perimeter of these shapes:

1. A  rectangle 7cm long by 8cm wide.

2. A square with one side 15cm long.

3. A rectangle 20cm by  30cm.

4. A  32cm by 10cm rectangle.

5. A rectangle 75cm  long by 25cm wide.

6. A  50cm by 50 cm square.

7. A rectangle 16cm by 12cm.

8. A  63cm by 25cm rectangle.

9. A square with one side measuring 45cm.

10. A rectangle 19cm long by 5cm wide

Exercise 2
Find the area and perimeter of each rectangle.
Remember to include the units in your answers.
(For example, m or square m)

1. 18 m wide, 23 m long
    perimeter = 
    area =  

2.  39 in wide, 30 in long
     perimeter = 
     area = 

3. 10 ft wide, 15 ft long
    perimeter =  
    area = 

4. 23 cm wide, 21 cm long
    perimeter = 
    area = 

5. 27 mm wide, 10 mm long
   perimeter = 
   area = 

6.  13 m wide, 46 m long
    perimeter = 
    area = 

7.  11 ft wide, 31 ft long
    perimeter =  
    area =  

8.  49 in wide, 8 in long
    perimeter = 
    area = 

9.  16 cm wide, 29 cm long
    perimeter = 
    area = 

10.  40 mm wide, 16 mm long
     perimeter = 
     area =  

HOW TO FIND THE ARES

To get the amount of space inside a figure, we use a square to represent 1 unit and we say that the area is measured in square units

Take a look at the following rectangle. To get the area, we are going to draw squares of equal sizes inside of it.



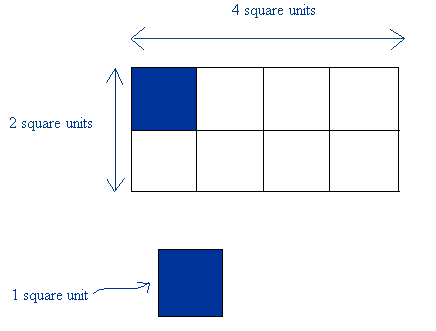
1 square represents 1 square unit. The rectangle has 8 squares, so the area for this rectangle is 8 square units.

We can also write 8 units² and it will mean the same

Notice,it is very important, that you can get the same answer if you multiply 2 square units by 4 square units because 2 × 4 = 8

2 square units represent the measure of the width and 4 square units represent the measure for the length.

Thus, in general, to get the area for a rectangle, just use the following formula:
Area of rectangle = length × width

THE SHAPES SONG....LALALALALA